Water has played a vital role in the advancement of mankind. The earliest traces of civilization reveal that those cultures which flourished were able to employ water sources for domestic, and agricultural purposes. A characteristic of all developed countries today is their ability to use productively the water made available to them.
- These open areas are figured for the entire grate. When determining actual flow areas, this should be reduced by the area of the seat. The net open area is calculated in square inches. RESTRICTED GRATE OPENINGS: When you design your project and you select a grate design, it is often necessary to consider slot size.
- Chanson reported that when the flow through culvert is flow type five then, in some cases, the inlet may act as an orifice and the discharge through the slot is calculated using the following equation: (2) Q o = N π D 2 4 2 g (H + P-y-h f) 1 2 where (N) is number of the weir openings, (Q o) is the theoretical discharge through opening L 3 /T.
- Online calculator to quickly determine Water Flow Rate through an Orifice. Includes 53 different calculations. Equations displayed for easy reference.
Weirs can be used to measure flow rates in open channels and rivers - common for water supply and sewage plants
Weirs are structures consisting of an obstruction such as a dam or bulkhead placed across the open channel with a specially shaped opening or notch. The flow rate over a weir is a function of the head on the weir.
Common weir constructions are the rectangular weir, the triangular or v-notch weir, and the broad-crested weir. Weirs are called sharp-crested if their crests are constructed of thin metal plates, and broad-crested if they are made of wide timber or concrete. If the notch plate is mounted on the supporting bulkhead such that the water does not contact or cling to the downstream weir plate or supporting bulkhead, but springs clear, the weir is a sharp-crested or thin-plate weir.
Water level-discharge relationships can be applied and meet accuracy requirements for sharp-crested weirs if the installation is designed and installed consistent with established ASTM and ISO standards.
Rectangular weirs and triangular or v-notch weirs are often used in water supply, wastewater and sewage systems. They consist of a sharp edged plate with a rectangular, triangular or v-notch profile for the water flow.
Broad-crested weirs can be observed in dam spillways where the broad edge is beneath the water surface across the entire stream. Flow measurement installations with broad-crested weirs will meet accuracy requirements only if they are calibrated.
Other available weirs are the trapezoidal (Cipolletti) weir, the Sutro (proportional) weir and the compound weirs (combination of the previously mentioned weir shapes). By combining V-notch weirs with broad chested weirs - larger range of flow can be measured with accuracy.
Rectangular Weir
The flow rate measurement in a rectangular weir is based on the Bernoulli Equation principles and can be expressed as:
q = 2/3 cd b (2 g)1/2 h3/2 (1)
where
q = flow rate (m3/s)
h = elevation head on the weir (m)
b = width of the weir (m)
g = 9.81 (m/s2) - gravity
cd = discharge constant for the weir - must be determined
cd must be determined by analysis and calibration tests. For standard weirs - cd - is well defined or constant for measuring within specified head ranges.
The lowest elevation (h = 0) of the overflow opening of the sharp-crested weirs or the control channel of broad-crested weirs is the head measurement zero reference elevation.
Rectangular Weir Flow Rate Measurement Calculator
cd - discharge constant
b - width of weir (m)
h - height of weir (m)
The Francis Formula - Imperial Units
Flow through a rectangular weir can be expressed in imperial units with the Francis formula
q = 3.33 (b - 0.2 h) h3/2 (1b)
where
Water Flow Through A Sponge
q = flow rate (ft3/s)
h = head on the weir (ft)
b = width of the weir (ft)
Alternative with height in inches and flow in gpm:
Triangular or V-Notch Weir
Water Flow Through A Slot Jackpots
The triangular or V-notch, thin-plate weir is an accurate flow measuring device particularly suited for small flows.
For a triangular or v-notch weir the flow rate can be expressed as:
q = 8/15 cd (2 g)1/2 tan(θ/2) h5/2 (2)
where
θ = v-notch angle
Broad-Crested Weir
For the broad-crested weir the flow rate can be expressed as:
q = cd h2 b ( 2 g (h1 - h2) )1/2 (3)
Measuring the Levels
For measuring the flow rate it's obviously necessary to measure the flow levels, then use the equations above for calculating. It's common to measure the levels with:
- ultrasonic level transmitters, or
- pressure transmitters
Ultrasonic level transmitters are positioned above the flow without any direct contact with the flow. Ultrasonic level transmitters can be used for all measurements. Some of the transmitters can even calculate a linear flow signal - like a digital pulse signal or an analog 4 - 20 mA signal - before transmitting it to the control system.
Pressure transmitters can be used for the sharp-crested weirs and for the first measure point in broad-crested weir. The pressure transmitter outputs a linear level signal - typical 4-20 mA - and the flow must be calculated in the transmitter or the control system.
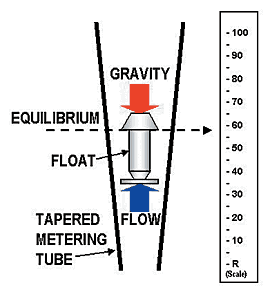
Related Topics
- Flow Measurement - Flow metering principles - Orifice, Venturi, Flow Nozzles, Pitot Tubes, Target, Variable Area, Positive Displacement, Turbine, Vortex, Electromagnetic, Ultrasonic Doppler, Ultrasonic Time-of-travel, Mass Coriolis, Mass Thermal, Weir V-notch, Flume Parshall and Sluice Gate flow meters and more
Related Documents
Water Flow Through A Small Block Chevy
- California Pipe Flow Metering Method - Measure discharge from the open end of partially filled horizontal pipes
- Comparing Flowmeters - A limited comparison of flowmeter principles - regarding service, rangeability, pressure loss, typical accuracy, upstream pipe diameters, viscosity and relative costs
- Flow Rate Calculated based on the Velocity-Area Principle - Flow rate or discharge in an open conduit, channel or river can be calculated with the velocity-area principle
- Flowmeters and Turndown Ratio - Rangeability - Turndown ratio for flow measurement devices like orifices, venturi meters etc.
- Froude Number - Introduction to the Froude Number
- Types of Fluid Flow Meters - An introduction to different types of fluid flowmeters - Orifices, Venturies, Nozzles, Rotameters, Pitot Tubes, Calorimetrics, Turbine, Vortex, Electromagnetic, Doppler, Ultrasonic, Thermal, Coriolis
- Waste Water - Flow Capacity - In sewage piping and pumping systems the fluid flow rate must be kept within certain limits to avoid operating problems
- Weirs - Flow Measurement Standards - Standards of weir flow measurements
Tag Search
- en: weirs notch v-notch flow measurement
- es: medición de flujo v-notch muesca vertederos
- de: Wehren Kerbe V-Kerbe-Durchflussmessung
This article provides calculation methods for correlating design, flow rate and pressure loss as a fluid passes through a nozzle or orifice. Nozzles and orifices are often used to deliberately reduce pressure, restrict flow or to measure flow rate.
| : | Diameter |
| : | Area |
| : | Discharge coefficient |
| : | Gravitational acceleration |
| : | Fluid head |
| : | Change in fluid head |
| : | Ratio of specific heats () |
| : | Pressure |
| : | Differential pressure () |
| : | Expansion coefficient (for incompressible flow) |
| : | Elevation |
| : | Ratio of pipe diameter to orifice diameter () |
| : | Mass density |
Subscripts
| : | Upstream of orifice or nozzle |
| : | Downstream of orifice or nozzle |
| : | Compressible fluid |
| : | Incompressible fluid |
| : | Orifice or nozzle |
| : | Static pressure |
In the case of a simple concentric restriction orifice the fluid is accelerated as it passes through the orifice, reaching the maximum velocity a short distance downstream of the orifice itself (the Vena Contracta). The increase in velocity comes at the expense of fluid pressure resulting in low pressures in the Vena Contracta. In extreme cases this may lead to cavitation when the local pressure is less than the vapour pressure of a liquid.
Downstream of the Vena Contracta in the recovery zone, the fluid decelerates converting excess kinetic energy into pressure as it slows. When the fluid has decelerated and returned to the normal bulk flow pattern the final downstream pressure has been reached.
The discharge coefficientcharacterises the relationship between flow rate and pressure loss based on the geometry of a nozzle or orifice. You can find typical values in our article on discharge coefficients for nozzles and orifices.
The relationships for flow rate, pressure loss and head loss through orifices and nozzles are presented in the subsequent section. These relationships all utilise the parameter, the ratio of orifice to pipe diameter which is defined as:
Where the point downstream of the orifice is sufficiently far away that the fluid has returned to normal full pipe velocity profile.
Horizontal Orifices and Nozzles
For orifices and nozzles installed in horizontal pipework where it can be assumed that there is no elevation change, head loss and flow rate may be calculated as follows:
| Property | Equation |
|---|---|
| Flow rate (in terms of) | |
| Flow rate (in terms of) | |
| Pressure loss | |
| Head Loss |
Vertical Orifices and Nozzles
For orifices and nozzles installed in vertical piping, with elevation change, the following head loss and flow rate equations may be used:
| Property | Equation |
|---|---|
| Flow rate (in terms of) | |
| Flow rate (in terms of) | |
| Pressure loss | |
| Head Loss |
Expansion Coefficient
The expansion coefficient takes account of the difference between the discharge coeffcicient for compressible and incompressible flows. It is defined as:
The expansion factoris typically determined empirically and can be calculated using one of the formulas below.
For incompressible fluids:
American Gas Association method as described in AGA 3.1:


Related Topics
- Flow Measurement - Flow metering principles - Orifice, Venturi, Flow Nozzles, Pitot Tubes, Target, Variable Area, Positive Displacement, Turbine, Vortex, Electromagnetic, Ultrasonic Doppler, Ultrasonic Time-of-travel, Mass Coriolis, Mass Thermal, Weir V-notch, Flume Parshall and Sluice Gate flow meters and more
Related Documents
Water Flow Through A Small Block Chevy
- California Pipe Flow Metering Method - Measure discharge from the open end of partially filled horizontal pipes
- Comparing Flowmeters - A limited comparison of flowmeter principles - regarding service, rangeability, pressure loss, typical accuracy, upstream pipe diameters, viscosity and relative costs
- Flow Rate Calculated based on the Velocity-Area Principle - Flow rate or discharge in an open conduit, channel or river can be calculated with the velocity-area principle
- Flowmeters and Turndown Ratio - Rangeability - Turndown ratio for flow measurement devices like orifices, venturi meters etc.
- Froude Number - Introduction to the Froude Number
- Types of Fluid Flow Meters - An introduction to different types of fluid flowmeters - Orifices, Venturies, Nozzles, Rotameters, Pitot Tubes, Calorimetrics, Turbine, Vortex, Electromagnetic, Doppler, Ultrasonic, Thermal, Coriolis
- Waste Water - Flow Capacity - In sewage piping and pumping systems the fluid flow rate must be kept within certain limits to avoid operating problems
- Weirs - Flow Measurement Standards - Standards of weir flow measurements
Tag Search
- en: weirs notch v-notch flow measurement
- es: medición de flujo v-notch muesca vertederos
- de: Wehren Kerbe V-Kerbe-Durchflussmessung
This article provides calculation methods for correlating design, flow rate and pressure loss as a fluid passes through a nozzle or orifice. Nozzles and orifices are often used to deliberately reduce pressure, restrict flow or to measure flow rate.
| : | Diameter |
| : | Area |
| : | Discharge coefficient |
| : | Gravitational acceleration |
| : | Fluid head |
| : | Change in fluid head |
| : | Ratio of specific heats () |
| : | Pressure |
| : | Differential pressure () |
| : | Expansion coefficient (for incompressible flow) |
| : | Elevation |
| : | Ratio of pipe diameter to orifice diameter () |
| : | Mass density |
Subscripts
| : | Upstream of orifice or nozzle |
| : | Downstream of orifice or nozzle |
| : | Compressible fluid |
| : | Incompressible fluid |
| : | Orifice or nozzle |
| : | Static pressure |
In the case of a simple concentric restriction orifice the fluid is accelerated as it passes through the orifice, reaching the maximum velocity a short distance downstream of the orifice itself (the Vena Contracta). The increase in velocity comes at the expense of fluid pressure resulting in low pressures in the Vena Contracta. In extreme cases this may lead to cavitation when the local pressure is less than the vapour pressure of a liquid.
Downstream of the Vena Contracta in the recovery zone, the fluid decelerates converting excess kinetic energy into pressure as it slows. When the fluid has decelerated and returned to the normal bulk flow pattern the final downstream pressure has been reached.
The discharge coefficientcharacterises the relationship between flow rate and pressure loss based on the geometry of a nozzle or orifice. You can find typical values in our article on discharge coefficients for nozzles and orifices.
The relationships for flow rate, pressure loss and head loss through orifices and nozzles are presented in the subsequent section. These relationships all utilise the parameter, the ratio of orifice to pipe diameter which is defined as:
Where the point downstream of the orifice is sufficiently far away that the fluid has returned to normal full pipe velocity profile.
Horizontal Orifices and Nozzles
For orifices and nozzles installed in horizontal pipework where it can be assumed that there is no elevation change, head loss and flow rate may be calculated as follows:
| Property | Equation |
|---|---|
| Flow rate (in terms of) | |
| Flow rate (in terms of) | |
| Pressure loss | |
| Head Loss |
Vertical Orifices and Nozzles
For orifices and nozzles installed in vertical piping, with elevation change, the following head loss and flow rate equations may be used:
| Property | Equation |
|---|---|
| Flow rate (in terms of) | |
| Flow rate (in terms of) | |
| Pressure loss | |
| Head Loss |
Expansion Coefficient
The expansion coefficient takes account of the difference between the discharge coeffcicient for compressible and incompressible flows. It is defined as:
The expansion factoris typically determined empirically and can be calculated using one of the formulas below.
For incompressible fluids:
American Gas Association method as described in AGA 3.1:
International Standards Organistion method as described in ISO 5167-2:
Article Tags